Introduction to Probability - The Science of Uncertainty
Probability models and axioms
Quantitative description: it is a description in terms of numbers
A probabilistic model is a quantitative description of a situation, a phenomenon, or an experiment whose outcome is uncertain.
Creating a model involves the following steps:
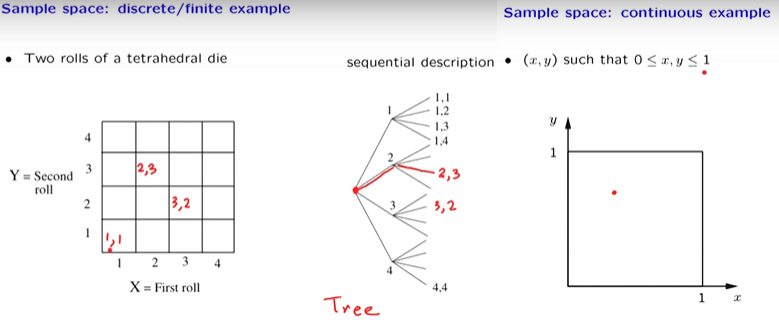
- Define the sample space: Describe the possible outcomes of the experiment (E.g. flip of a coin, roll a dice, etc.), composed of
- Sample spaces are sets which can be discrete, finite, infinite, continuous (recorded with infinite precision)...
- List (
set) of the possible outcomes ($\Omega$), the elements of the set must be:
- Mutually Exclusive: At end of experiment there can only be one of the outcomes of the set
- Collectively Exhaustive: Together all the elements of the set exhaust all the possibilities, at the end of the experiment you should be able to select one from the set
- At the 'right' Granularity includes only the different outcomes in what we are considering relevant and not different in irrelevant outcomes. E.g. in the flip a coin example the sample space (set) would be Heads=0 or Tails=1, instead of Heads & Rain=0, Heads & No Rain=1, Tails & Rain=2, Tails & No Rain=3, whether is raining it's irrelevant, we only include what is relevant
- Specify a probability law which assigns probabilities to outcomes or to collection of outcomes, the probability law specifies which outcomes are more likely to occur and which are less likely
- Probability is usually assigned to events (an event is a subset of the sample space). We assign probabilities to the various subsets of the sample space.
- Probabilities are given between 0 (practically cannot happen) and 1 (practically certain event will happen)
- Probabilities have certain axioms or basic properties (axioms: unprovable rule or principle accepted as true) for example probabilities cannot be negative.
- Axioms of probability:
- Non-negativity: Probabilities are positive $P(A) \ge 0$
- Normalization: We are certain event Omega will occur $P(\Omega) = 1$
- Additivity The probability that the outcome of the experiments falls in Event A or B is equal to the sum of the
probabilities of these two sets.

- There are probabilistic experiments that can be described in stages (E.g two rolls of a tetrahedral die), these type of experiments can be represented using a sequential tree or description
Properties of Probabilities

- if $A$ is subset of $B$ the probability that event $B$ occurs ($P(B)$) must be greater or equal than the probability that event $A$ occurs
$$A \subset B \Rightarrow P(A) \le P(B)$$
$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

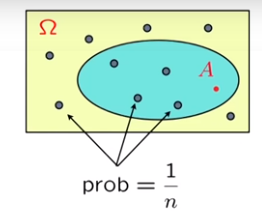
- Discrete Uniform Probability Law
- A finite sample space consist of $n$ equally likely elements
- The probability that event $A$ occurs which can be set of $k$ outcomes is $P(A) = \dfrac{k}{n}$
Probability calculations steps:
- Specify sample space (values of the outcomes)
- Specify probability law
- Identify the probability of an event of interest
- Calculate
There are two kinds of infinte sets: 1) discrete (countable) which are set whose elements can be arranged in a sequence like the integers and 2) uncountable sets whose elements cannot be arranged in a sequence
Probabilities can be interpreted as frequencies: the frequency with which certain event will occur in a infinite number of repetitions of the experiment
Probabilities are oftenly used informally to decribe beliefs or likelihood of events
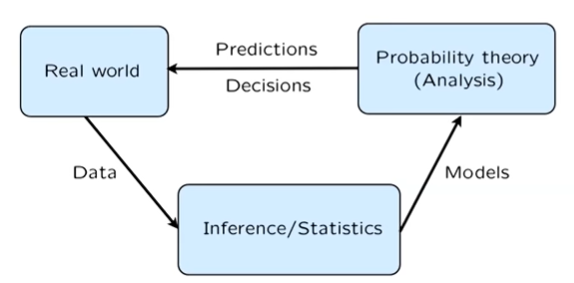
Probability gives a set of rules to think systematically about uncertain situations which can be used as tool to make predictions and decisions
Real World generates data, statistics uses this data to come up with probabilistic models, we use probaility theory and this model to make predictions and desicions about the real world
Math Background and Refresher for Probability
Sets

De Morgarn's Law
- The complement of the intersection of two sets is equal to the union of the complemenet of each individual set
$$(S \cap T)^c = S^c \cup T^c$$
- The complement of a union is the same as the intersection of the complements
$$(S \cup T)^c = S^c \cap T^c$$
- De Morgan's law extended to multiple sets and allows us to go back and forth between unions and intersections

Sequence
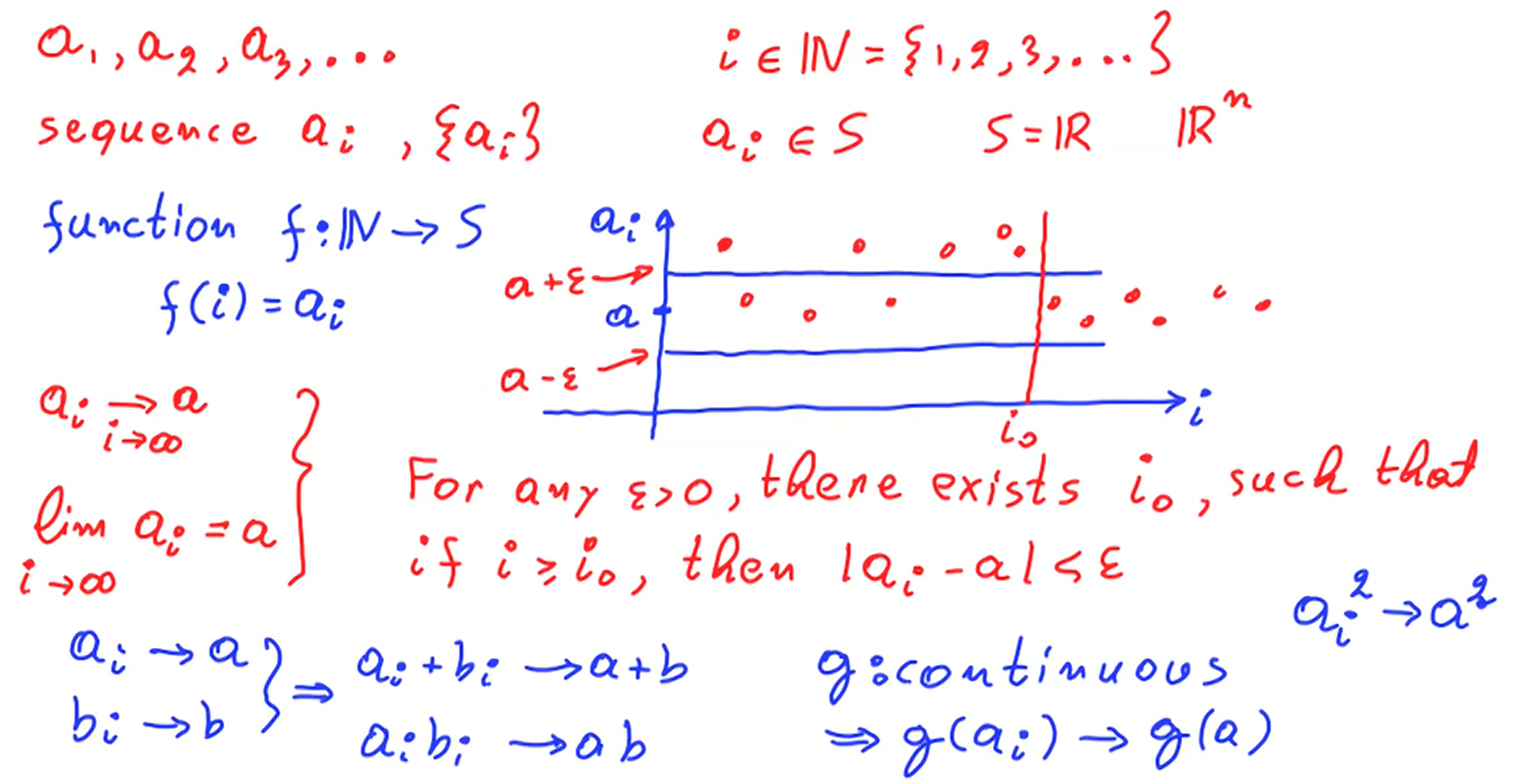
A sequence is a collection of elements that are coming out of some set and that collection of elements is indexed by the natural numbers (positive integers)
Formally it is a function that to any natural number assigns an element of a set ($S$)
We usually want to know if a sequence converge, this means we whant to know if as the index tends to infinity the sequence tends to an specifici number.
Formally what it means that a sequence converge is that if we plot the sequence as a function of $i$ as $i$ tends to infinity the values of $a_i$ get and stay inside a small band (defined by \epsilon)
if a sequence converge we can assume certain properties like the multiplication, sum or application of a function can be applied to the value the sequence(s) converge
- When we have a sequence that keep increasing (in math terms this means $a_i \leq a_{i+1}) the sequence converges to infinity
- When we have a sequence that keeps getting closer to a certain value as $i$ increases we say it converges to some real number $a$, in math termsn $|a_i -a| \leq b_i$ and $b \rarrow 0$ then $a_i \larr a$
Infinite Series
- Inifinite series are the infinite sum of a sequence in math terms
$$ \sum_{i=1}^{\inf} a_i =\lim_{n\rightarrow\infty} \sum_{i=1}^n a_i $$
Geometric Series
- It is an infinite series that shows in many examples and applications
- It is the sume of all the powers of a certain number which absolute value is less than 1 ($|\alpha| < 1$)
$$ \sum_{i=0}^{\inf} \alpha^i = 1 +\alpha + \alpha^2 + ... = \dfrac{1}{1-\alpha} $$
References









