Want to show support?
If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...
If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...
Tal que cumpla con una cierta propiedad usamos $ : $ o $ / $
Cuantificador existencial ($\exists $): Usado para decir que existe un cierto elemento
Cuantificador existencia y Unicidad ($\exists !$): Usado para decir que un elemento existe y es único
Cuantificador Universal / Para todos ($\forall$): Usado para decir que para todos los elementos de un conjunto se cumple una cierta propiedad
Pertenece ($\in$): Usado para decir que un elemento $x$ pertenece o esta incluido en un conjunto
No Pertenece ($\notin$): Usado para decir que un elemento $x$ no pertenece a conjunto $A$
Inclusión de conjuntos ($\subset$):significa estar contenido en por lo que $A \subset B$ significa que el conjunto $A$ esta incluido en $B$
Inclusión e igualdad de conjuntos ($\subseteq$):significa estar contenido en o ser igual por lo que $A \subseteq B$ significa que el conjunto $A$ esta incluido o es igual al conjunto $B$
Ejemplo: Para todo $x$ existe un $y$ (que pertenece a los reales) tal que $x$ más $y$ es igual a cero. Se escribe: $\forall x \exists y \in \mathbb{R} : x + y = 0$
Un conjunto es una colección de objetos distintos (no ordenados), es decir se puede encontrar números, palabras, letras, etc. (denotados con letras mayúsculas)
Los objetos que están en un conjunto se denomina elementos (denotados con letras minúsculas)
Formas de determinar, definir o especificar un conjunto:
Dos conjuntos son iguales cuando tienen exactamente los mismos elementos (el orden no importa y los elementos son únicos)
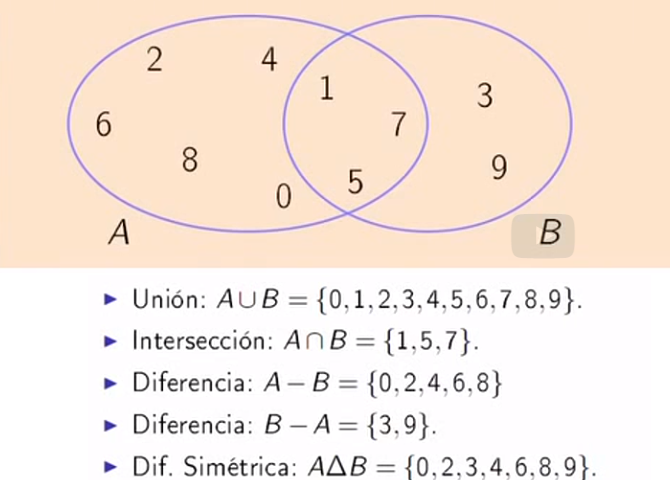
Diagramas de Venn son una representación graficas de un conjunto
Un conjunto $A$ está incluido en $B$ si todos los elementos de $A$ están en $B$ (No se necesitamos que todos los elementos de $B$ estén en $A$). Si $A \subset B$ decimos que $A$ es un subconjunto de $B$
El conjunto vacío es un conjunto con cero elementos y por ende siempre es subconjunto de otro conjunto
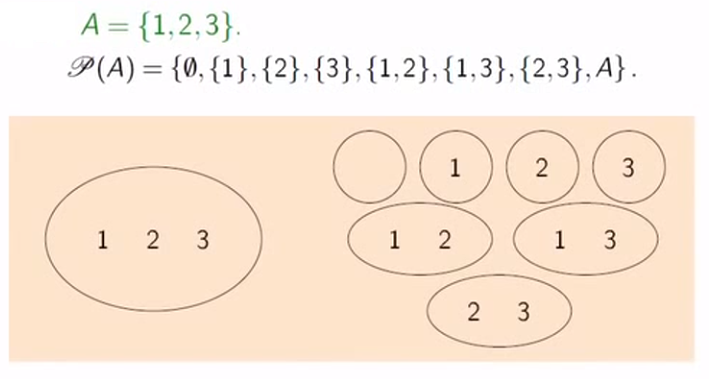
Dado un conjunto $A$ las partes de A ($\mathscr{P}(A)$) se refiere a un nuevo conjunto donde los elementos son todos los subconjuntos de $A$ (incluyéndose a si mismo y al conjunto vacío)
Un Sistema de Numeración es un conjunto de normas y reglas para escribir y trabajar con números
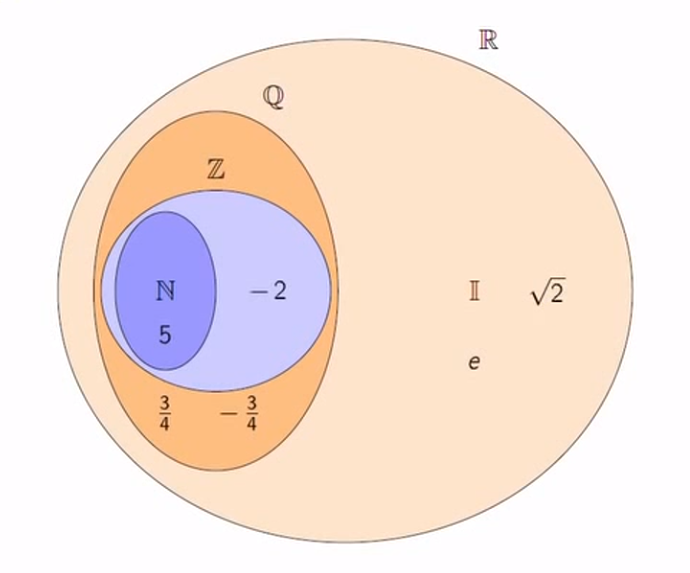
Los Números Naturales ($\mathbb{N}$) es el conjunto de los números con los que se cuenta o contabiliza (Solo incluye los positivos) $\mathbb{N} = \{0,1,2,3,4,5,...\}$
Los Números Enteros ($\mathbb{Z}$) es el conjunto de los números naturales mas los numero naturales cambiados de signo $\mathbb{Z} = \{\pm a: a \in \mathbb{N} \} = \{...,-3,-2,-1,0,1,2,3,...\}$
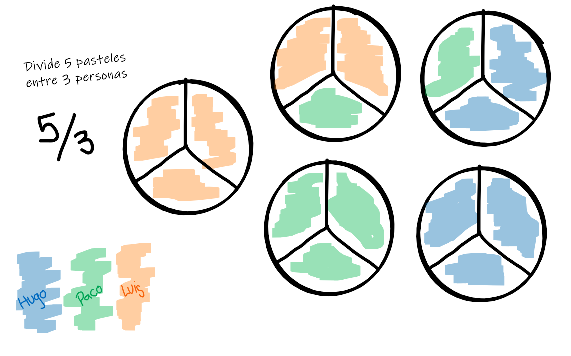
Los Números Racionales ($\mathbb{Q}$) es el conjunto de los números fraccionales $\mathbb{Q} = \left\{ \dfrac ab : a,b \in \mathbb{Z}, b \ne 0 \right\} $ $a$: numerador $b$: denominador. Se pueden expresar como Decimales ($\mathbb{D}$) Exactos (Ejemplo: $\frac 52 = 2.5$) o Periódicos (Ejemplo: $\frac 53 = 1 + \frac 23 = 1.6666 \cdots = 1.\overparen{6}$)
| Generalización | Ejemplo |
|---|---|
| $a^0 = 1$ | $2^0=1$ |
| $a^1 = a$ | $2^1=2$ |
| $a^m = a \cdot a \overset{\rm m}{\rm \cdots} a$ | $2^5=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2=32$ |
| $a^{-n} = \dfrac {1}{a^n}$ | $2^{-1}=\dfrac {1}{2}$ |
| $a^p \cdot a^q = a^{p+q}$ | $2^2 \cdot 2^3=2^5=32$ |
| $\dfrac{a^p}{a^q} = a^{p-q}$ | $\dfrac {2^2}{2^3}=2^{-1}=\dfrac {1}{2}$ |
| $(a^p)^q = a^{p \cdot q}$ | $(2^3)^2 = 2^{2 \cdot 3}=2^6=64$ |
| $a^p \cdot b^p = (a \cdot b)^p$ | $2^2 \cdot 3^2=6^2=36$ |
| $\dfrac{a^p}{b^p} = \left(\dfrac{a}{b}\right)^p$ | $\dfrac{2^2}{3^2} = \left(\dfrac{2}{3}\right)^2$ |
| $\sqrt[n]{a} = a^{\frac{1}{n}}$ | $\sqrt[3]{8}=8^{\frac{1}{3}}=(2^3)^{\frac{1}{3}}=2$ |
| $\sqrt[n]{a^m} = (\sqrt[n]{a})^m = a^{\frac{m}{n}}$ | $ \sqrt[3]{2^3} = 2^{\frac{3}{3} = 2} $ |
| $(a+b)^2 = a^2+2ab+b^2$ | $(x+1)^2 = x^2+2x+1$ |
| $(a-b)^2 = a^2-2ab+b^2$ | $(x-1)^2 = x^2-2x+1$ |
| $(a+b)(a-b) = a^2-b^2$ | $(x+1)(x-1) = x^2-1$ |
Al conjunto de los números complejos se denota como $\mathbb{C}$
Hay muchas ecuaciones que no podemos resolver trabajando solo con números reales. Por ejemplo:
Al numero $\sqrt{-1}$ se le denomino numero imaginario representándolo como $i$ y esta demostrado que con la raíz cuadrada de $-1$ se puede resolver cualquier ecuación (Gauss 1799) creada con la combinación de números reales y complejos
$$i = \sqrt{-1}$$ $$i^2 = -1$$
Siendo $z=z_1=a+ib$ ; $z_2=c+id$
| Operación | Generalización |
|---|---|
| Suma | $z_1+z_2=(a+b)+i(c+d)$ |
| Resta | $z_1-z_2=(a-b)+i(c-d)$ |
| Producto | $z_1 \cdot z_2=(ac-bd)+i(ad+bc)$ |
| Inverso | $z^{-1}=\dfrac{1}{z} =\left(\dfrac{a}{a^2+b^2}\right)+i\left(\dfrac{-b}{a^2+b^2}\right) = \dfrac{a-ib}{a^2+b^2} = \dfrac{\overline z}{|z|^2} $ |
| División Siendo $z_2 \ne 0$ |
$\dfrac{z_1}{z_2} =z_1 \cdot z_2^{-1} =\left(\dfrac{ac+bd}{c^2+d^2}\right)+i\left(\dfrac{bc-ad}{c^2+d^2}\right)$ |
| Conjugado Misma Parte Real Parte Imaginaria Opuesta |
$\overline z = a - ib$ |
| Producto Conjugado | $z \cdot \overline z = a^2 + b^2$ |
| Modulo 'Valor real' |
$|z| = \sqrt{a^2+b^2}$ |
| Modulo Cuadrado | $|z|^2 = a^2+b^2 = z \cdot \overline z $ |
| Modulo Conjugado | $|z| = |\overline z| $ |
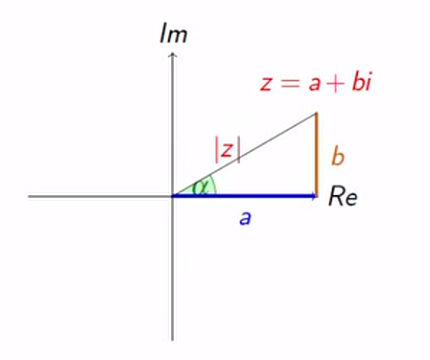
$$ \sin{\alpha}=\dfrac{b}{|z|}$$ $$ \cos{\alpha}=\dfrac{a}{|z|}$$ $$ \tan{\alpha}=\dfrac{\sin{\alpha}}{\cos{\alpha}}=\dfrac{b}{a}$$ $$ arg(z) = \alpha = \arctan{\left(\frac{|b|}{|a|}\right)}$$


| Forma | Expresión | Ejemplo |
|---|---|---|
| Binómica | $z=a+ib$ | $z=1+i$ |
| Cartesiana | $z=(a,b)$ | $z=(1,1)$ |
| Trigonométrica | $z=|z| (\cos{\alpha}+i\sin{\alpha})$ $z=r (\cos{\alpha}+i\sin{\alpha})$ |
$|z|=r=\sqrt{1^2+1^2}=\sqrt{2}$ $\alpha=\arctan{(1)}=\pi/4$ $z=\sqrt{2} (\cos{\frac\pi4}+i\sin{\frac\pi4}) $ |
| Polar | $z=r_{\alpha}$ | $z=\sqrt{2}_{\frac\pi4}$ |
$$x = \dfrac{-b ± \sqrt{b^2-4ac}}{2a}$$
$$a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x = b $$
Pata ecuaciones de primer grado basta con despejar, con ecuaciones de segundo grado usualmente se usa la formula general y para ecuaciones de grado superior se puede graficar y ver las intersecciones en cero o usar la Regla de Ruffini
La solución o soluciones de una ecuación se refiere a el valor o los valores de las incógnitas que hacen que se cumpla la igualdad

Una ecuación lineal de $n$ incógnitas $x_1,x_2,\ldots,x_n$ es una igualdad en la que las incógnitas no están elevadas a ninguna potencia ni como argumento de otras funciones matemáticas, es decir es del tipo: $$a_11x_1+a_2x_2+\ldots+a_nx_n=b$$
Un sistema ecuaciones lineales de $m$ ecuaciones con $n$ incógnitas $x_1,x_2,\ldots,x_n$ es un conjunto de $m$ igualdades de la forma
$$ \left\lbrace\eqalign{a_{11}x_1+a_{12}x_2+ \cdots + a_{1n}x_n &= b_1 \cr a_{21}x_1+a_{22}x_2+ \cdots + a_{2n}x_n &= b_2 \cr \cdots \cdots \cdots \cr a_{m1}x_1+a_{m2}x_2+ \cdots + a_{mn}x_n &= b_m \cr}\right\rbrace$$
$$A_{m \times n}=\left(\begin{array}{c & c & c & c} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \cr a_{2,1} & a_{2,2} & \cdots & a_{2,n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m,1} & a_{m,2} & \cdots & a_{m,n} \cr \end{array}\right) $$
Operaciones con Matrices:
Tipos de Matrices:
Método de Gauss Método para resolver sistemas de ecuaciones que consiste en resolver el sistema mediante transformaciones, es decir multiplicar una ecuación del sistema, luego sumarla a otra para eliminar una de las incógnitas. Buscamos crear ceros por debajo de la diagonal de la matriz lo que resulta en un sistema de ecuaciones equivalente pero mas sencillo del cual podemos despejar directamente la incógnita $x_n$, sustituir en otra ecuación del sistema este valor, obtener la incógnita $x_{n-1}$ y así sucesivamente
$$G_M=\pmatrix{ a_{1,1} & a_{1,2} & a_{1,3} & \ldots & a_{1,{n-1}} & a_{1,n} & b_1 \cr 0 & a_{2,2} & a_{2,3} & \ldots & a_{2,{n-1}} & a_{2,n} & b_2\cr 0 & 0 & a_{3,3} & \ldots & a_{3,{n-1}} & a_{3,n} & b_3\cr \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots\cr 0 & 0 & 0 & \ldots & a_{{m-1},{n-1}} & a_{{m-1},n} & b_{m-1}\cr 0 & 0 & 0 & \ldots & 0 & a_{m,n} & b_m\cr }$$
- Si el sistema tiene solución única se puede dejar con ceros abajo de la diagonal
- Si el sistema tiene múltiples soluciones (infinitas) el ultimo renglón da todo ceros
- Si el sistema no tiene solución en el ultimo renglón da una igualdad errónea por ejemplo $0=b_m$
$$det(A_{2 \times 2})=\left|\begin{array}{c & c &} a_{1,1} & a_{1,2} \cr a_{2,1} & a_{2,2} \cr \end{array}\right| = a_{1,1}a_{2,2} - a_{1,2}a_{2,1} $$
$$det(A_{3 \times 3})=\left|\begin{array}{c & c & c} a_{1,1} & a_{1,2} & a_{1,3} \cr a_{2,1} & a_{2,2} & a_{2,3} \cr a_{3,1} & a_{3,2} & a_{3,3} \cr \end{array}\right| = a_{1,1}a_{2,2}a_{3,3} + a_{1,3}a_{2,1}a_{3,2} + a_{1,2}a_{2,3}a_{3,1} - a_{1,3}a_{2,2}a_{3,1} - a_{1,1}a_{3,2}a_{2,3} - a_{3,3}a_{1,2}a_{2,1} $$
Matriz Inversa y Regular ($A^{-1}$) matriz que cumple $A^{-1}A=AA^{-1}=I$. Para calcularla:

Regla de Cramer Es un método para resolver sistemas de ecuaciones a través de las determinantes

If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...