Want to show support?
If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...
If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...
Algebra is arithmetic that includes non-numerical entities like x
If we have exponents on variables ($x^2 = 4$) or other non linear function it isn't linear algebra because it describes non-linear shapes in a graph
Linear algebra deals with system of linear equations
Linear algebra we have one solution, no solutions or infinite solutions
Regression models aim to establish a relationship between the input features and the target variable, allowing predictions of continuous values to be made.
Tensor vector or matrix of any number of dimensions
We can represent vectors using its coordinates [1,2] but also its magnitude
Norms are functions that allow us to quantify the vector magnitude (also called length), the most common is teh L^2 Norm (Pythagoras or Ecludian distance from origin)
$$\lvert\lvert x \rvert\rvert = \lvert\lvert x \rvert\rvert_2 = \sqrt{\sum_{i}x^2_i}$$
$$\lvert\lvert x \rvert\rvert^2_2= {\sum_{i}x^2_i} = x^T \cdot x$$
So a unit vector is a special case of vector where its length is equal to one ||x||=1
Max Norm $L^\infty$ Norm returns the absolute value of the largest magnitude element.
$$\lvert\lvert x \rvert\rvert_\infty = max_i\lvert x_i \rvert$$
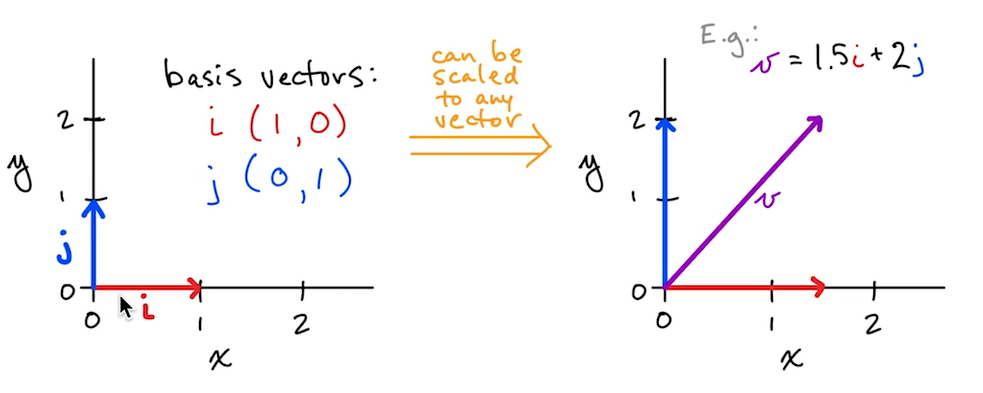
Orthogonal Vectors two vectors are orthogonal if $x^T \cdot y = 0$
Orthonormal Vectors are a special type of Orthogonal vectors where their $L^2 = 1$ for example basis vectors are
Generic Tensor $X_{(i,j,k,l)}$, for example images are sually represented with 4-tensor -Example $X_{(2, 4, 4, 3)}$ 2 images; max of 4 pixels of height ; max of 4 pixels of width 3 values for RGB, each element is a pixel ina gigen image )
Mutiply, add, substract by scalar applies to all elements of tensor and shape remains
Element-wise product $ A \bigodot X $
Reduction Sum the sum across all elements of a tensor
Dot Product: Creates a scalar value by calculating the product of elements with same index and sum them all
Matrix multiplication left matrix has same number of columns as right matrix has rows (multiply rows for columsn and sum)
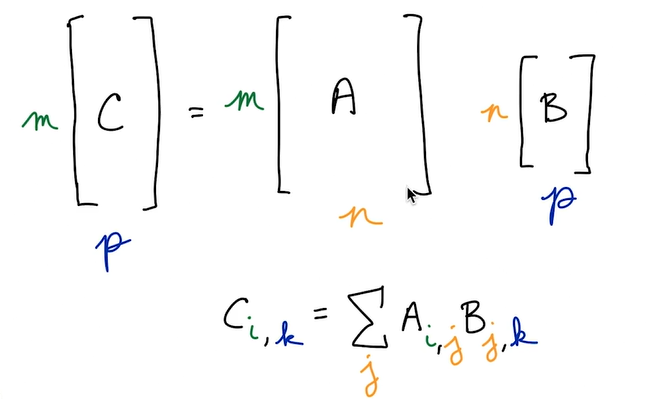
If you find the information in this page useful and want to show your support, you can make a donation
Use PayPal
This will help me create more stuff and fix the existent content...